在深度学习中，我们“训练”模型，不断更新它们，使它们在看到越来越多的数据时变得越来越好。 通常情况下，变得更好意味着最小化一个损失函数（loss function）， 即一个衡量“模型有多糟糕”这个问题的分数。 最终，我们真正关心的是生成一个模型，它能够在从未见过的数据上表现良好。 但“训练”模型只能将模型与我们实际能看到的数据相拟合。 因此，我们可以将拟合模型的任务分解为两个关键问题：

  • 优化（optimization）：用模型拟合观测数据的过程；
  • 泛化（generalization）：数学原理和实践者的智慧，能够指导我们生成出有效性超出用于训练的数据集本身的模型。

导数和微分

在深度学习中，我们通常选择对于模型参数可微的损失函数。 简而言之，对于每个参数， 如果我们把这个参数增加或减少一个无穷小的量，可以知道损失会以多快的速度增加或减少，假设我们有一个函数f:R→R，其输入和输出都是标量。 如果f的导数存在，这个极限被定义为

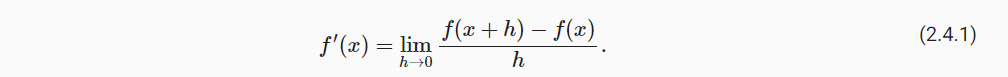
1724549062760

先回顾一下微积分的知识中常见的求微分规则：

1724543590466

以及一些求微分中常用的法则：

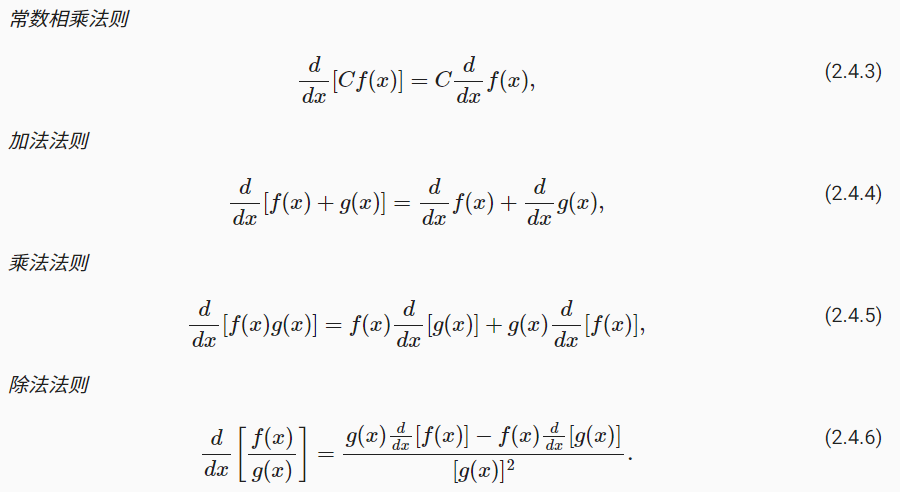
1724549248635

偏导数

将微分的思想推广到多元函数上:

1724549392562

梯度向量

我们可以连结一个多元函数对其所有变量的偏导数，以得到该函数的梯度（gradient）向量。 具体而言，设函数 f : Rn→R 的输入是 一个n维向量x=[x1,x2,…,xn]⊤，并且输出是一个标量。 函数f(x)相对于x的梯度是一个包含n个偏导数的向量:

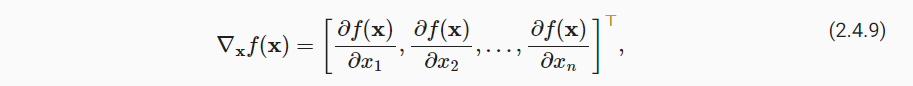
1724549623298

假设x为n维向量，那么在微分多元函数时我们经常使用以下规则：

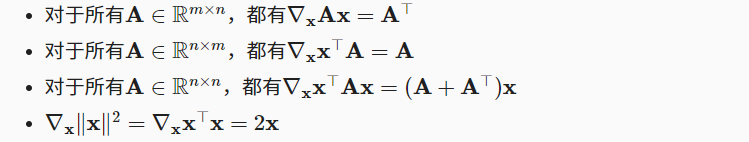
1724549692203

链式法则

但是上面的方法可能很难找到梯度，因为在深度学习中，多元函数通常是复合函数，而为了解决问题，我们一般会使用链式法则来微分复合函数。

首先考虑单变量函数。假设有 y = f (u) 和 u = g (x) 这两个函数，且可微分，则：

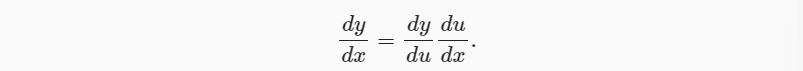
1724549976454

而如果是考虑多变量函数。假设可微分函数 y 有变量 u1 , u2 , u3 , … , um ，而其中每个可微分函数 ui 都有变量 x1 , x2 , x3 , … , xn，且 y 是 x1 , x2 , x3 , … , xn 的函数。则对于任意 i = 1 , 2 , … , n，由链式法则可得出：

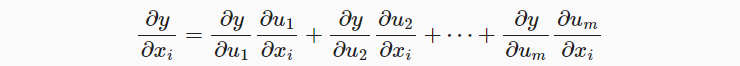
1724550177731

标量和向量的微分矩阵

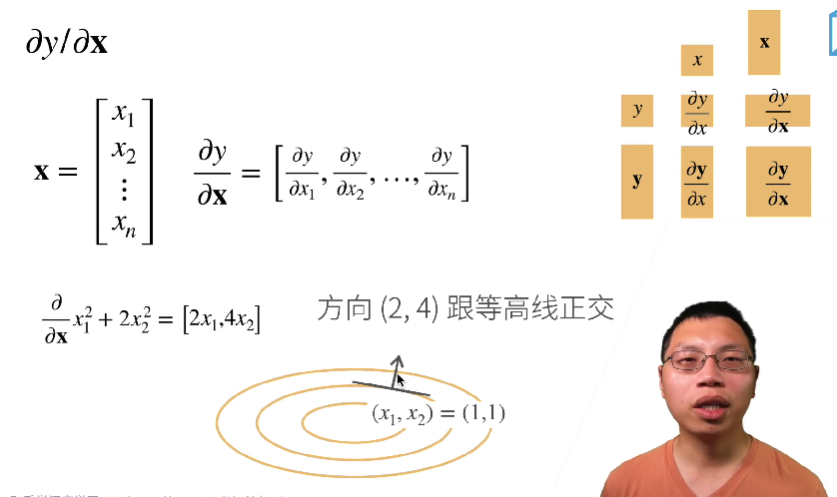
然而神经网络的函数求导可能有几百层，所以我们一般要用自动求导。

自动微分

深度学习框架通过自动计算导数，即自动微分（automatic differentiation）来加快求导。 实际中，根据设计好的模型，系统会构建一个计算图（computational graph）， 来跟踪计算是哪些数据通过哪些操作组合起来产生输出。 自动微分使系统能够随后反向传播梯度。 这里，反向传播（backpropagate）意味着跟踪整个计算图，填充关于每个参数的偏导数。 每个圈表示一个操作

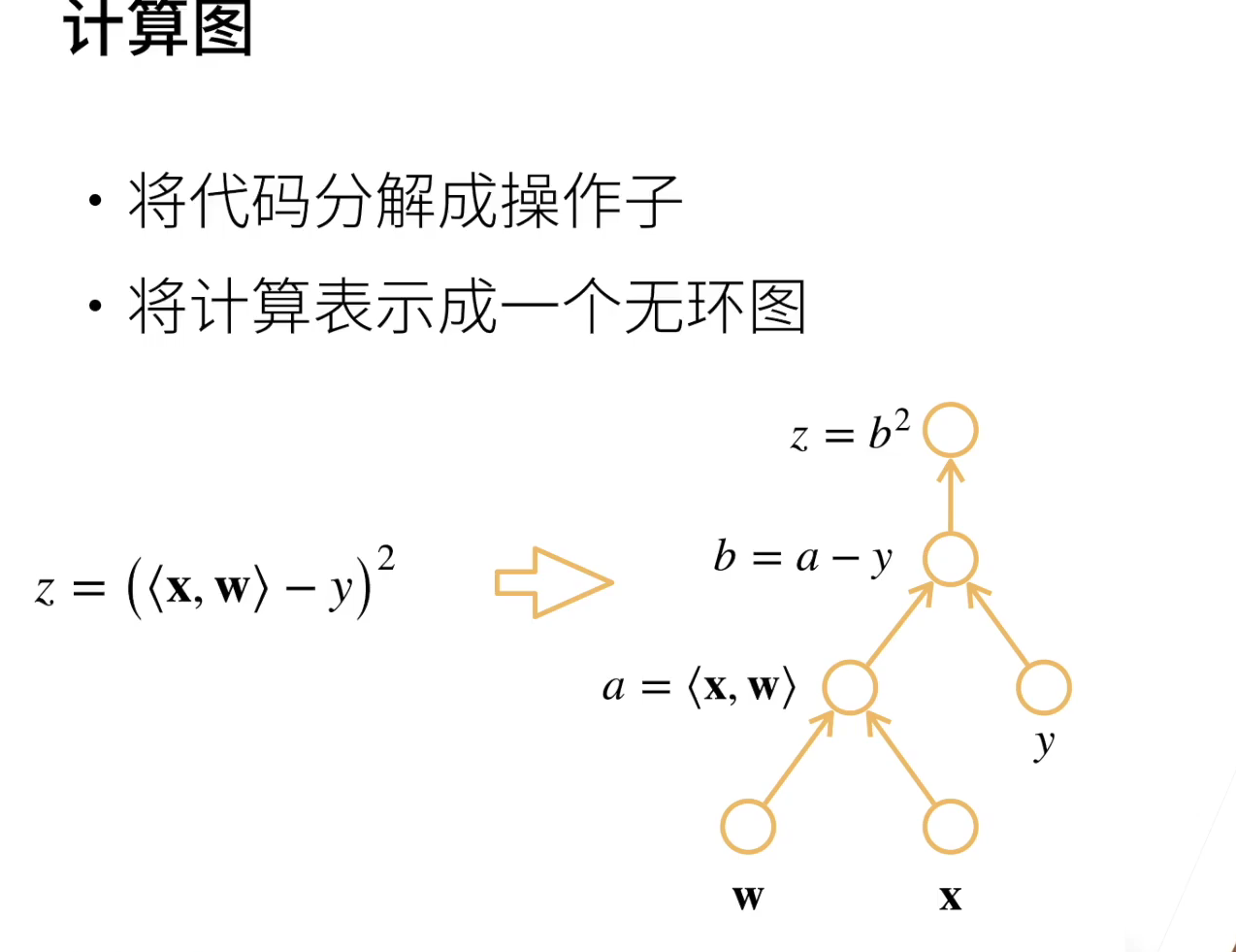
1724544288707

在我们计算y关于x的梯度之前，需要一个地方来存储梯度。 重要的是，我们不会在每次对一个参数求导时都分配新的内存。 因为我们经常会成千上万次地更新相同的参数，每次都分配新的内存可能很快就会将内存耗尽。 注意，一个标量函数关于向量x的梯度是向量，并且与x具有相同的形状。

自动求导的两种模式：

1724544420082

反向累计

计算图示：

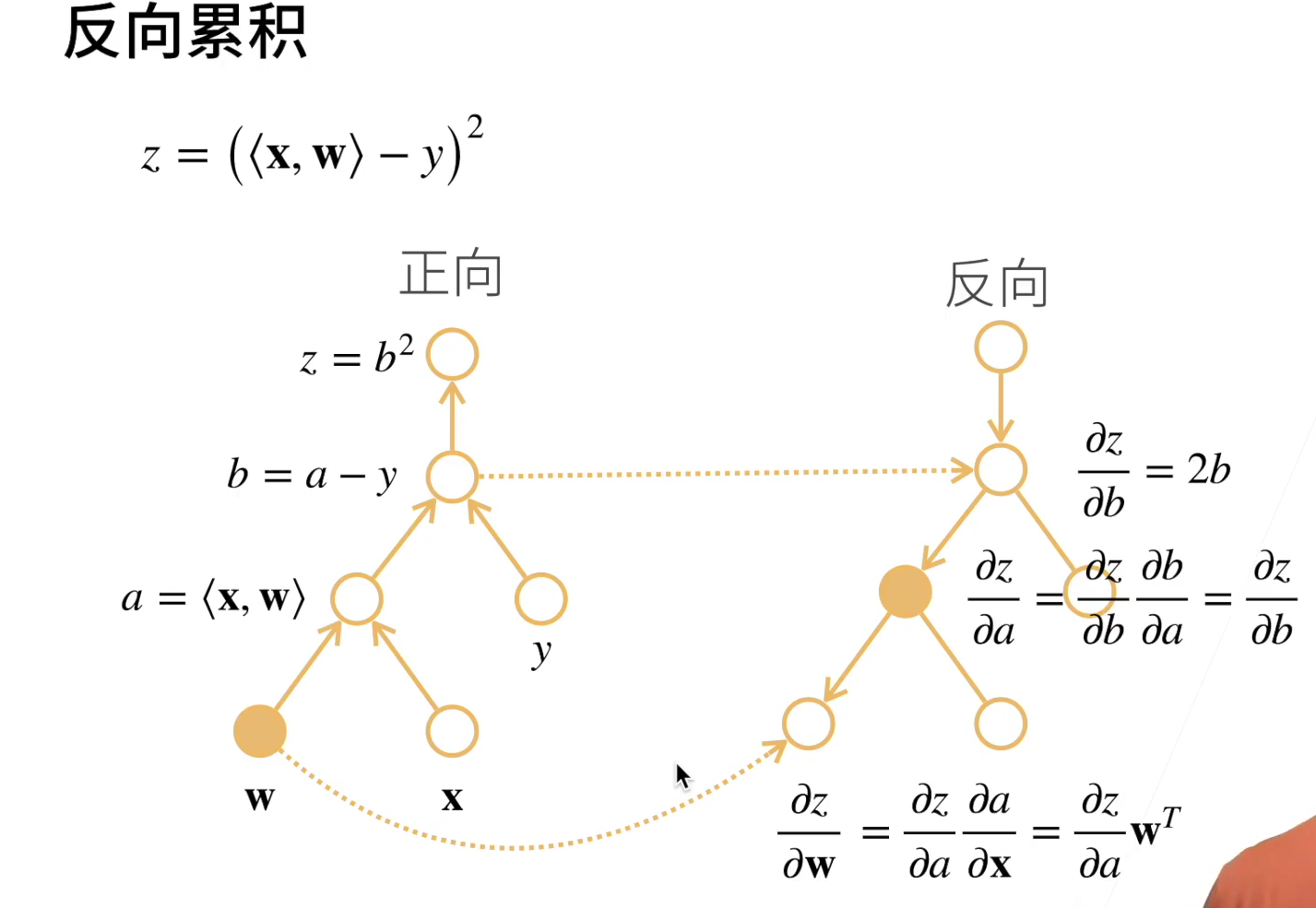
1724544478318

之所以更多选择的是反向累积，是因为：

1724544515808

实例代码演示（这里默认了使用pytorch）：

1
2
3
4
5
6
import torch

x = torch.arange(4.0) # 首先创建向量x，并分配初始值 [0., 1., 2., 3.]
x.requires_grad_(True) # 等价于x=torch.arange(4.0,requires_grad=True)
x.grad  # 默认值是None
y = 2 * torch.dot(x, x) #计算y （dot是点乘）

x是一个长度为4的向量，计算x和x的点积，得到了我们赋值给y的标量输出。 接下来，通过调用反向传播函数来自动计算y关于x每个分量的梯度，并打印这些梯度。 

1
2
3
4
5
6
7
y.backward()
x.grad 
#打印出来的结果为 tensor([ 0.,  4.,  8., 12.])
#而 y = 2 x·x 函数对于x的求导就应该是 y'(x)= 4x
#代入验证
x.grad == 4 * x
#打印结果显示 tensor([True, True, True, True])

就说明这个梯度向量计算出来是正确的。

现在计算x的另一个函数，但是注意，在默认情况下，PyTorch会累积梯度，我们需要清除之前的值。

1
2
3
4
5
x.grad.zero_() #清除梯度
y = x.sum()
y.backward()
x.grad
#打印出来的结果：tensor([1., 1., 1., 1.])

Q：如果没有清除梯度，会怎么样？

A：就会在原来的梯度向量的基础上累加本次计算得出的梯度向量，如下：

1724551675852