Abstract

本文开发了一种方法，从学生过去的活动中识别出与给定 knowledge concept (KC) 相关的 KC，并根据它选择的相对较少的 KC 来预测他/她的掌握程度。由于预测是基于相对较少的过去活动进行的，因此它比基于 RNN 的方法更好地处理数据稀疏性问题。为了确定 KC 之间的相关性，我们提出了一种基于自我注意的方法，即自我关注知识追踪 （SAKT）。

Introduction

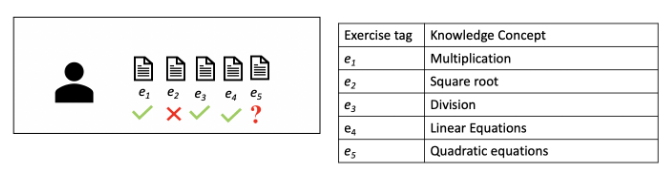
左子图显示了学生尝试的练习顺序，右子图显示了每个练习所属的知识概念。

知识追踪 （KT） 被认为是一项重要的任务，被定义为根据学生过去的学习活动追踪学生的知识状态的任务，该知识状态代表他/她对 KC 的掌握水平。KT 任务可以正式化为监督序列学习任务 - 给定学生过去的运动互动 X = （x1， x2， . . . ， xt），预测他/她下一次互动的某个方面 xt+1。在问答平台上，交互表示为 xt = （et， rt），其中 et 是学生尝试时间戳 t 的练习，rt 是学生答案的正确性。知识转移旨在预测学生是否能够正确回答下一个练习，即预测 p（rt+1 = 1|et+1， X）

最近深度学习模型，如深度知识追踪 （DKT）及其变体使用递归神经网络 （RNN） 在一个汇总的隐藏向量中对学生的知识状态进行建模。动态键值记忆网络 （DKVMN）利用记忆增强神经网络进行知识转移。它使用两个矩阵，键和值，分别学习练习与底层 KC 和学生知识状态之间的相关性。DKT 模型面临其参数不可解释的问题。DKVMN 比 DKT 更具可解释性，因为它显式维护 KC 表示矩阵（键）和知识状态表示矩阵（值）。然而，由于所有这些深度学习模型都是基于 RNN 的，因此它们在处理稀疏数据时面临着不泛化的问题。

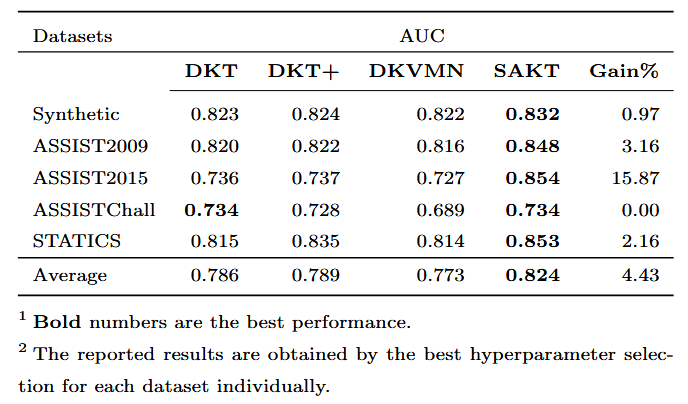
本文提出的 SAKT 首先从过去的互动中识别相关的 KC，然后根据他/她在这些 KC 上的表现预测学生的表现。为了预测学生在练习中的表现，我们使用练习作为 KC。正如我们稍后展示的那样，SAKT 为先前回答的练习分配权重，同时预测学生在特定练习中的表现。所提出的 SAKT 方法明显优于最先进的 KT 方法，在所有数据集中，AUC 的性能平均提高了 4.43%。此外，SAKT 的主要组件 （self-attention） 适用于并行;因此，我们的模型比基于 RNN 的模型快一个数量级。

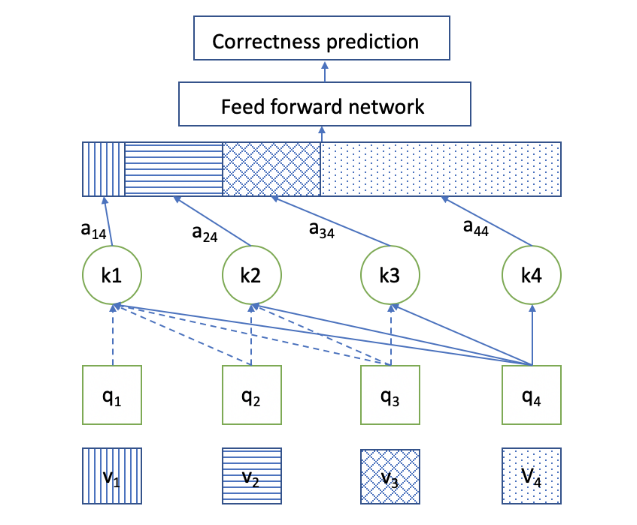
1727665621262

上图为SAKT 网络。在每个时间戳中，仅针对前一个元素估计关注权重。键、值和查询是从如下所示的嵌入层中提取的。当第 j 个元素是 query 且第 i 个元素是 key 时，注意力权重为 ai，j。

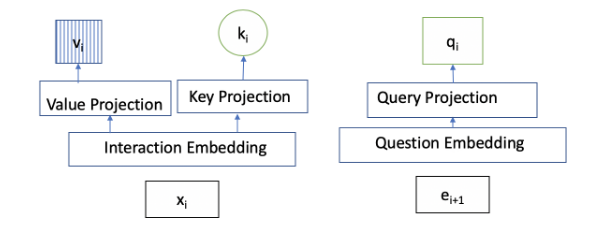
1727665760632

Embedding layer嵌入了学生正在尝试的当前练习和他过去的交互。在每个时间戳 t+1 时，当前问题 et+1 使用 Exercise 嵌入嵌入到查询空间中，并且过去交互的元素 xt 嵌入到 th 中。

x是交互，e是练习，r是正确性，

Proposed method

我们的模型根据学生之前的交互序列 X = x1， x2， . . . ， xt 预测学生是否能够回答下一个练习 et+1。如图 2 所示，我们可以将问题转化为顺序建模 表 1：符号 符号 描述 N 学生总数 E 练习总数 X 学生的交互序列：（x1， x2， . . . ， xt） 习 学生的第 i 对练习-答案对 n 序列的最大长度 d 潜在向量维数 e 学生解决的练习序列 M 交互嵌入矩阵 P 位置嵌入矩阵 E 练习查找矩阵 ˆM过去的互动嵌入 ˆE 运动嵌入问题。考虑输入 x1， x2， . . . ， xt−1 的模型和领先一个位置的练习顺序 e2， e3， . . . ， et 很方便，输出是对练习 r2， r3， . . . ， rt 的反应的正确性。交互元组 xt = （et， rt） 以数字 yt = et + rt × E 的形式呈现给模型，其中 E 是练习总数。因此，交互序列中的元素可以采用的总值为 2E，而 exercise 序列中的元素可以采用 E 个可能的值。

嵌入层：我们将得到的输入序列 y = （y1， y2， . . . ， yt） 转换为 s = （s1， s2， . . . ， sn），其中 n 是模型可以处理的最大长度。由于模型可以使用固定长度序列的输入，如果序列长度 t 小于 n，我们会在序列左侧重复添加问答对的填充。但是，如果 t 大于 n，我们将序列划分为长度为 n 的子序列。具体来说，当 t 大于 n 时，yt 被划分为长度为 n 的 t/n 子序列。所有这些子序列都用作模型的 Input。
我们训练一个交互嵌入矩阵 M ∈ R^2E×d^，其中 d 是潜在维度。此矩阵用于获取序列中每个元素 s^i^ 的嵌入 M^si^。 同样，我们训练练习嵌入矩阵 E ∈ R^E×d^，使得集合 e^i^中的每个练习都嵌入到第 e^i^ 行中。

位置编码：位置编码是自注意力神经网络中的一层，用于对位置进行编码，以便像卷积网络和递归神经网络一样，我们可以对序列的顺序进行编码。这一层在知识追踪问题中尤为重要，因为学生的知识状态会随着时间的推移逐渐稳定地发展。为了整合这一点，我们使用了一个参数，位置嵌入，P ∈ Rn×d，它是在训练时学习的。然后将位置嵌入矩阵的第 i 行 Pi 添加到交互序列第 i 个元素的交互嵌入向量中。

嵌入层的输出是嵌入式交互输入矩阵 ˆM 和嵌入式练习矩阵 ˆE.（如下图）

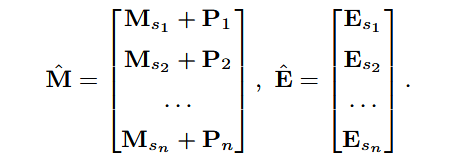
1727689570808

自注意层：在我们的模型中，我们使用了缩放的点积注意力机制 。此层查找与先前解决的每个练习相对应的相对权重，以预测当前练习的正确性。 我们使用以下方程获得查询和键值对：
$$
Q = \widehat { E } W ^ { Q } , K = \widehat { M } W ^ { K } , V = \widehat { M } W ^ { V }
$$
其中 WQ、WK、WV ∈ Rd×d 分别是查询、键和值投影矩阵，它们将各自的向量线性投影到不同的空间 。之前每个交互与当前练习的相关性是使用注意力权重确定的。为了找到注意力权重，我们使用缩放的点积 ，定义为：
$$
A t t e n t i o n ( Q , K , V ) = s o t t i m a x ( \frac { Q K ^ { T } } { \sqrt { d } } ) V
$$
多头：为了共同关注来自不同代表性子空间的信息，我们使用不同的投影矩阵线性投影查询、键和值 h 次。
$$
M u l t i h e a d ( \widehat { M } , \widehat { E } ) = C o n c a t ( h e a d _ { 1 } , \ldots , h e a d _ { h } ) W ^ { O }
$$
在预测 （t + 1） st 练习的结果时，我们应该只考虑第一个 t 个交互。因此，对于查询 Qi，不应考虑 j > i 的键 Kj。我们使用因果层来掩盖从未来的交互键中学到的权重（ Causality layer是一种神经网络中的层，它用于处理时间序列数据。在因果层中，网络的输出仅依赖于当前和过去的输入，而不依赖于未来的输入。这种特性使得因果层能够捕捉到时间序列数据的因果关系，从而更好地预测未来的趋势。 ）

前馈层：上述自注意力层导致值的加权和，即先前交互的 Vi。但是，从多头层获得的矩阵行 S = Multihead（ ˆM， ˆE） 仍然是先前交互作用的值 Vi 的线性组合。为了在模型中加入非线性并考虑不同潜在维度之间的相互作用，我们使用了前馈网络。
$$
F = F F N ( S ) = R e L U ( S W ^ { ( 1 ) } + b ^ { ( 1 ) } ) W ^ { ( 2 ) } + b ^ { ( 2 ) }
$$
其中 W（1） ∈ Rd×d、W（2） ∈ Rd×d、b（1） ∈ Rd、b（2） ∈ Rd 是在训练期间学习的参数。

残差连接：残差连接 用于将较低层特征传播到较高层。因此，如果低层特征对于预测很重要，则残差连接将有助于将它们传播到执行预测的最终层。在 KT 的背景下，学生尝试属于特定概念的练习以加强该概念。因此，残差连接可以帮助将最近解决的练习的嵌入传播到最后一层，使模型更容易利用低层信息。残差连接在 self-attention 层和 Feed Forward 层之后应用。

层归一化：在 [[1]](https://github.com/chrispiech/DeepKnowledgeTracing/tree/ master/data/synthetic) 中，表明跨特征归一化输入有助于稳定和加速神经网络。出于相同的目的，我们在架构中使用了层归一化。图层标准化也应用于自注意力层和前馈图层。

预测层：最后，上面得到的矩阵 Fi 的每一行都通过激活 Sigmoid 的全连接网络来预测学生的表现。
$$
p _ { i } = S i g m o i d ( F _ { i } w + b )
$$
其中 pi 是一个标量，代表学生对练习 ei 提供正确反应的概率，Fi 是 F 的第 i 行。
$$
S i g m o i d ( z ) = 1 / ( 1 + e ^ { - z } )
$$
网络训练：训练的目标是最小化模型下观察到的学生反应序列的负对数似然。这些参数是通过最小化 pt 和 rt 之间的交叉熵损失来学习的。
$$
C = - \sum _ { t } ( r _ { t } \log ( p _ { t } ) + ( 1 - r _ { t } ) \log ( 1 - p _ { t } ) )
$$

Experience settings

指标：预测任务被视为二元分类设置，即正确或否回答练习。因此，我们使用曲线下面积 （AUC） 指标来比较性能。

方法：我们将我们的模型与最先进的 KT 方法 DKT [6] 、 DKT + [10] 和 DKVMN [11] 进行了比较。这些方法在简介中进行了介绍。 模型训练和参数选择：我们使用 80% 的数据集训练模型，并在剩余数据集上进行测试。对于所有方法，我们尝试了隐藏状态维度 d = {50， 100， 150， 200}。对于竞争方法，我们使用了与他们各自论文中报告的相同的超参数。对于权重的初始化和优化，我们使用了与 [10] 类似的过程。我们使用 Tensorflow 实现 SAKT，并使用学习率为 0.001 的 ADAM [5] 优化器。我们对 ASSISTChall 数据集使用了 256 的批次大小，对其他数据集使用了 128 的批次大小。对于记录数量较多的数据集，例如 ASSISTChall 和 ASSIST2015，我们使用的丢失率为 0.2，而对于其余数据集，我们使用的丢失率为 0.2。我们设置序列的最大长度 n 与每个学生的平均锻炼标签大致成正比。对于 ASSISTChall 和 STATICS 数据集，我们使用 n = 500，对于ASSIST2009 n = 100 和 50 ，对于合成数据集和 ASSIST2015 数据集 n 设置为 50。

1728029584075

消融实验

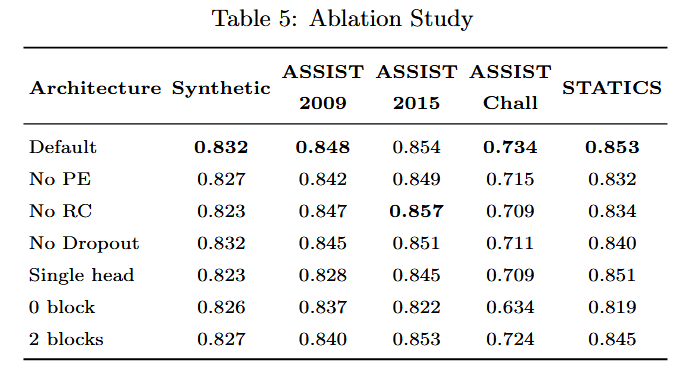
1728030331307
  • RC 对模型的性能没有太大贡献。事实上，删除残差连接可提供比 ASSIST2015 数据集的默认值更好的性能。
  • 无 Dropout：Dropout 在神经网络中用于正则化模型，以便它可以更好地泛化。与模型的参数数量相比，模型的过拟合对于记录数较少的数据集更有效。因此，dropout 的角色对 ASSIST2009 数据集和 STATICS 数据集更有效。
  • 单头：我们尝试了仅使用 1 个 head 的变体，而不是默认架构中那样使用 5 个 head。多个 head 有助于捕获不同子空间中的注意力权重。使用单个磁头会持续降低 SAKT 在所有数据集上的性能。
  • 无块：当不使用自我注意力块时，下一个练习的预测仅取决于最后一次交互。可以看出，没有 attention block 的性能明显差于默认架构。
  • 2 个区组：增加自我注意区组的数量会增加模型的参数数量。然而，在我们的例子中，这种参数的增加并没有被证明对提高性能有用。之所以是预测学生在练习中表现的一个重要方面，取决于他在过去相关练习中的表现。添加另一个自我注意块会使模型更加复杂。

Conclusion and Future work

在这项工作中，我们提出了一种基于自我注意力的知识追踪模型 SAKT。它对学生的交互历史进行建模（不使用任何 RNN），并通过考虑他过去交互中的相关练习来预测他在下一个练习中的表现。对各种真实数据集的广泛实验表明，我们的模型可以胜过最先进的方法，并且比基于 RNN 的方法快一个数量级。

Source Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np


import torch
import torch.nn as nn
import numpy as np

class sakt(nn.Module):  # 定义一个名为sakt的类，继承自PyTorch的nn.Module模块
    def __init__(self, ex_total, seq_len, dim, heads, dout):
        super(sakt, self).__init__()  # 调用父类的构造函数
        self.seq_len = seq_len  # 序列长度
        self.dim = dim  # 嵌入向量的维度

        # 交互嵌入层：将输入数据转换为嵌入向量
        self.embd_in = nn.Embedding(2 * ex_total + 1, embedding_dim=dim)
        # 练习嵌入层：将输入数据转换为嵌入向量
        self.embd_ex = nn.Embedding(ex_total + 1, embedding_dim=dim)
        # 位置嵌入层：为序列中的 每个位置生成一个嵌入向量
        self.embd_pos = nn.Embedding(seq_len, embedding_dim=dim)

        # 线性投影层：对嵌入向量进行线性变换，这里有三个线性层，从dim维映射到dim维，参数可以变换
        self.linear = nn.ModuleList([nn.Linear(in_features=dim, out_features=dim) for x in range(3)])
        # 多头注意力机制：捕捉序列中的依赖关系
        self.attn = nn.MultiheadAttention(embed_dim=dim, num_heads=heads, dropout=dout)
        # 前馈神经网络：进一步处理注意力输出
        self.ffn = nn.ModuleList([nn.Linear(in_features=dim, out_features=dim, bias=True) for x in range(2)])

        # 输出层：将最终的输出转换为预测值
        self.linear_out = nn.Linear(in_features=dim, out_features=1, bias=True)
        # 层归一化：对输出进行归一化处理，帮助神经网络更好地训练
        self.layer_norm1 = nn.LayerNorm(dim)
        self.layer_norm2 = nn.LayerNorm(dim)
        # Dropout层：随机丢弃一些神经元，防止过拟合
        self.drop = nn.Dropout(dout)

    def forward(self, input_in, input_ex):
        # 位置嵌入：为序列中的每个位置生成一个嵌入向量
        pos_in = self.embd_pos(torch.arange(self.seq_len).unsqueeze(0))

        # 获取交互嵌入输出：将输入数据转换为嵌入向量并加上位置嵌入
        out_in = self.embd_in(input_in)
        out_in = out_in + pos_in

        # 分离交互嵌入：将其分为v和k（需要验证是否已分离）
        value_in = out_in
        key_in = out_in

        # 获取练习嵌入输出：将输入数据转换为嵌入向量
        query_ex = self.embd_ex(input_ex)

        # 对所有嵌入进行线性投影：将嵌入向量转换为相同的维度
        value_in = self.linear[0](value_in).permute(1, 0, 2)
        key_in = self.linear[1](key_in).permute(1, 0, 2)
        query_ex = self.linear[2](query_ex).permute(1, 0, 2)

        # 通过多头注意力层：计算注意力权重并更新查询向量
        atn_out, _ = self.attn(query_ex, key_in, value_in, attn_mask=torch.from_numpy(np.triu(np.ones((self.seq_len, self.seq_len)), k=1).astype('bool')))
        atn_out = query_ex + atn_out  # 残差连接：将原始查询向量与注意力输出相加
        atn_out = self.layer_norm1(atn_out)  # 层归一化：对注意力输出进行归一化处理

        # 调整批次维度的顺序：将批次放在第一个维度上
        atn_out = atn_out.permute(1, 0, 2)

        # 前馈神经网络：对注意力输出进行进一步处理
        ffn_out = self.drop(self.ffn[1](nn.ReLU()(self.ffn[0](atn_out))))
        ffn_out = self.layer_norm2(ffn_out + atn_out)  # 残差连接和层归一化

        # 输出层：将最终的输出转换为预测值（介于0和1之间）
        ffn_out = torch.sigmoid(self.linear_out(ffn_out))

        return ffn_out


          
def randomdata():
    input_in = torch.randint( 0 , 49 ,(64 , 12) )
    return input_in, input_in



## Testing the model 
E =  50 # total unique excercises
d = 128 # latent dimension
n = 12  # sequence length

d1,d2 = randomdata()

print( 'Input shape',d1.shape)
model = sakt( ex_total= E , seq_len= n , dim= d , heads= 8, dout= 0.2 )
out = model( d1, d2)
print('Output shape', out.shape)